Sophelen Research

In this post, we will use logistic regression to assess the health of our aquaponic system. Here, we will discuss ways we can handle imbalance classes. We will work with an aquaponics dataset that has already been cleaned and artificially transformed to be more natural (yes, oxymoron). We already created a column called at_risk using guidelines from FAO.

TLDR: Among the methods in handling imbalance classes for this particular data, balancing the weights is the simplest and most effective. Undersampling actually did quite well, though not surprising given the majority class has a lot of redundant rows.

Though I could also use the weight column to assess the health of the system, I am ignoring it for now as I don’t enough about aquaculture. Furthermore, it would be difficult to implement the fish weight as the fish would be harvested in staggered intervals.

df_clean['at_risk'] = 0
at_risk_mask = (df_clean.ph < 5.5) | (df_clean.ph > 8.5) |  (df_clean.nh3 > 3) | (df_clean.no3 > 300) | (df_clean.do < 4)
df_clean.loc[at_risk_mask, 'at_risk'] =1

df = spark.read.format("delta").load("Tables/clean_pond")
df = df.toPandas().set_index('date')
df.head(5)

In the table above, at_risk is 1’s because the dissolved oxygen is a bit low. About 86% (5487) of the rows are not at risk, while 14% (8863) of the rows are at risk. Let’s bring in a few libraries:

import pandas as pd 
import numpy as np 
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc, precision_recall_curve, average_precision_score, classification_report
from imblearn.over_sampling import SMOTE

X=df.iloc[:,:-2]
y=df.iloc[:,-1]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)

As mentioned above, we have imbalanced classes in our dataset. We will discuss various ways in handling imbalanced classes: assigning weights to the loss function, undersampling the majority class (I do not like this one at all), oversampling the minority class, and oversampling the minority class intelligently with SMOTE from imblearn library. Note that if you wish to use SMOTE, make sure to apply it to training data only to avoid data leakage. This is true whenever you perform some kind of black box transformation to your data.

Let’s first discuss handling imbalanced classes using class weight. If we use logistic regression from sklearn, there is an option for class weight: LogisticRegression(class_weight=’balanced’). We will brieftly outline how class_weight works.

Each sample x from X is of the form

From the post Logistic regression in simple terms, there is a probability function p that is the composition of the following two functions

Furthermore, the loss function is given by

We wish to find two weights, w_0 for class 0 and w_1 for class 1 such that w_1 is heavier than w_0, and they should equal to 1 when the classes are balance. Intuitively, the weights should be inversely proportional to their sizes. I’m sure there are various ways to define the weights, but a canonical way to define them is

,

where N_0 and N_1 are the number of samples in class 0 and class 1, respectively. Computing specifically for our aquaponics data, we obtain

So now the new loss function is

Let’s look at the classification report for logistic regression with class weight and without class weight, respectively.

lr_weight = LogisticRegression(class_weight='balanced')
lr_weight.fit(X_train,y_train)
y_prop = lr_weight.predict_proba(X_test)[:,1]
y_pred = lr_weight.predict(X_test)
print(classification_report(y_test,y_pred))

lr=LogisticRegression()
lr.fit(X_train,y_train)
y_pred0 = lr.predict(X_test)
print(classification_report(y_test,y_pred0))

Comparing the recall scores, the model with balanced class weights handles the minority class much better than the model without balanced class weights.

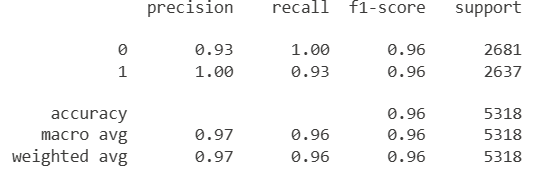
There are two other common methods handling imbalance classes: undersampling and oversampling. For oversampling, we will perform both with and without SMOTE. Let’s look at the classification reports for all three.

majority_class = df[df.at_risk==0]
minority_class = df[df.at_risk==1]
under_majority_class = resample(majority_class, replace=False, 
n_samples = len(minority_class), random_state=123)
undersampling_df = pd.concat([under_majority_class,minority_class])
X=undersampling_df.iloc[:,:-2]
y=undersampling_df.iloc[:,-1]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
lr=LogisticRegression()
lr.fit(X_train,y_train)
y_pred = lr.predict(X_test)
print(classification_report(y_test,y_pred))

majority_class = df[df.at_risk==0]
minority_class = df[df.at_risk==1]
over_minority_class = resample(minority_class, replace=True, 
n_samples = len(majority_class), random_state=123)
oversampling_df = pd.concat([majority_class,over_minority_class])
X=oversampling_df.iloc[:,:-2]
y=oversampling_df.iloc[:,-1]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
lr=LogisticRegression()
lr.fit(X_train,y_train)
y_pred = lr.predict(X_test)
print(classification_report(y_test,y_pred))

From the classification reports, the undersampling technique outperforms the oversampling technique. As much as I do not like undersampling because we are losing data, it still can be useful. Now, let’s look at SMOTE. Now, since I am using SMOTE as a black box oversampling technique, I need to split my data first to avoid data leakage. See application of SMOTE from Microsoft Learn.

X=df.iloc[:,:-2]
y=df.iloc[:,-1]
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
smote = SMOTE(random_state=123)
X_train_smote,y_train_smote = smote.fit_resample(X_train,y_train)
lr=LogisticRegression()
lr.fit(X_train_smote,y_train_smote)
y_pred = lr.predict(X_test)
print(classification_report(y_test,y_pred))

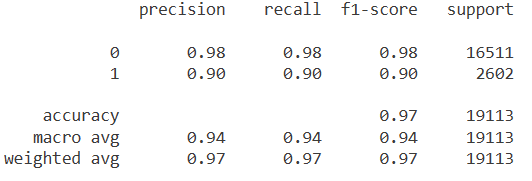
CONCLUSION: Ranking by recall for class 1: adjusting class weights (95%), undersampling (93%), oversampling (91%), SMOTE (90%), no adjustments (85%). So, in this particular case, adjusting class weights is simple and effective.